Calculs sur caps & relèvements

Résumé. chapitre 3 page 4

Formules et calculs entre Zc et Zv en 7 images.
Formules et calculs entre Cv et Cc en 6 images.
Petit truc d'un Granvillais naviguant en Manche
Utilisation de la rose des vents pour calculer la déclinaison.
Utilisation de la courbe de déviation pour calculer la déviation
Rappel : Les règles du calcul algébrique

Formules et calculs entre Zc et Zv en 7 images.

Zv = Zc+W ou Zc=Zv-W

Explications des calculs en 7 images.
Maintenant étudions les relations algébriques qui existent entre les Zc et Zv. Nous avons la formule Zv = Zc +W ou Zc = Zv - W. Dans votre cas, nous employons la première.
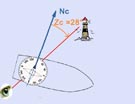
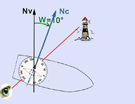
Image N° 1 : Zc = 28° dans ce cas.
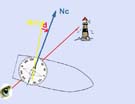
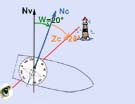
Image N° 2 : Nous faisons apparaître Nm et d qui est "Est" et égale à 10° donc = +10°
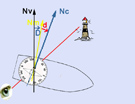
Image N° 3 : Nous faisons apparaître Nv et D est "Est" et égale à 10° donc = +10°.
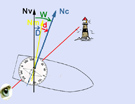
Image N° 4 : W=D+d. W=+10°+(+10°)= +20° ( positif donc "Est")
Image N° 5 : W= 20°
Image N° 6 : Zc= 28° W =20°
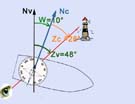
Image N° 7 : Zv = Zc+W = 28° +(+20°) = 48° + 20° = 48°. Zv = 48°

Formules et calculs entre Cv et Cc en 6 images.

Comment calculer son cap compas pour naviguer entre Granville et Saint-malo.

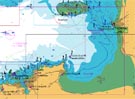
Aujourd'hui, le temps est beau et nous avons décidé de passer le week end à Saint-malo depuis Granville. L'équipage est prêt à faire une belle balade.
Sur ma carte numérique( image jointe), le logiciel Seapro donne un cap vrai de 240°. Sur les cartes, nous travaillons avec le Nord géographique et nous obtenons un cap vrai.
Cv = 240°. Quel cap compas donnerons nous au barreur pour qu'il nous emmène vers Saint Malo?
Avertissement : les D et d sont fausses pour simplifier la construction des images.
Maintenant nous représentons le Cv sur la première image.

Cv = Cc+W ou Cc=Cv-W

Explications des calculs en 6 images.
Maintenant étudions les relations algébriques qui existent entre les Cc et Cv. Nous avons la formule Cv = Cc +W ou Cc = Cv - W. Nous employons la seconde.
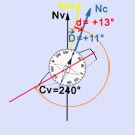
Image N° 1 : CV = 240° dans ce cas.
Image N° 2 : Nous faisons apparaître Nm et D qui est "Est" et égale à 11° donc = +11°
Remarquons que le fond des images a changé. Sur la précédente, le fond représente une carte, maintenant il est bleu comme la mer (Nous travaillons avec le nord compas).
Image N° 3 : Nous faisons apparaître Nc et d est "Est" et égale à 13° donc = +13°.
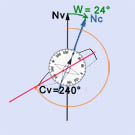
Image N° 4 : W=D+d. W=+13°+(+11°)= +24° ( positif donc "Est")
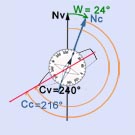
Image N° 5 : W= 24° et Cc=Cv-W= 240° -(+24°) = 216°
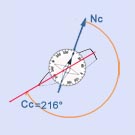
Image N° 6 : Cc= 216 °
Nous proposons au barreur "Cap au 216 .

Utilisation de la rose des vents pour calculer la déclinaison.

Prenons la carte de Chausey et agrandissez l’image en cliquant dessus. Une flèche inclinée vers le NW avec un angle. Des chiffres et des lettres nous renseignent :


4° 10’ valeur de la déclinaison
W Ouest donc négative
- 4° 10' valeur en 1995
7 variation de 7'par an
E Variation E dans ce cas, une diminution de sa valeur
Calcul de la déclinaison pour 2005.
2005 – 1995 = 10 ans
Variation 7 *10 = 70’. 1° = 60'1° 10 est équivalant 70'
Valeur 2005 4° 10’ - 1° 10’ = 3°. Comme la Déclinaison est ouest, sa valeur est négative.

En 2005 D= -3°.

Autre calcul
La déclinaison sera nulle en 2031 (180/7= 26 ans).

Utilisation de la courbe de déviation pour calculer la déviation

Imaginons que nous naviguons vers Granville et sur la carte nous avons trouvé un cap vrai de 110°
Quel sera le cap compas à donner au barreur ?
Cc = Cv – W.
Il faut toujours calculer la valeur intermédiaire: le Cap magnétique (Cm).
Précédemment, la déclinaison a une valeur de 3° W ou -3°.
Cm = Cv – D ou 110° -(- 3°) = 110° + 3°= 113°
Sur la courbe de déviation, pour un cap de 113° nous trouvons une déviation de 3° 30’ positive à droite.
Cc = CM – d ou 113° - 3° 30’ = 109° 30’
En résumé W = D +d = - 3° + (+ 3° 30’) = + 0 ° 30’
Cc = Cv – W = 110° -(+ 0° 30’) = 109° 30.
Nous prendrons comme cap compas 110°


Rappel : Les règles du calcul algébrique
Dans une addition de 2 nombres de même signe, il faut ajouter les 2 nombres et donner au résultat le signe commun.
Exemple: -8 + (- 4) = -12
Signe commun négatif, résultat négatif.
Signe commun positif résultat positif.
Dans une addition de 2 nombres de signes contraires, il faut retrancher le plus petit du plus grand et donner au résultat le signe du plus grand.
Exemple: -8 + (+ 15) = + 7
Signe du plus grand positif, résultat positif).
Signe du plus grand négatif, résultat négatif).
Dans une soustraction de 2 ou plusieurs signes algébriques, inverser le signe du 2e et des autres nombres, ainsi que celui de l'opération et appliquer les règles précédentes.
Exemple: -5- (- 4) est équivalent à- 5 + (+ 4).





Truc mnémotechnique

Truc mnémotechnique pour retenir « Est plus, Ouest moins » :

Question : Est-ce plus ou est-ce moins = EST plus OUEST moins ?

Page mise à jour le 17 août 2018

Ce site (textes, plans, images) est soumis aux droits Creative Commons: